Category: Dataphile Posts
Root category for site posts
-

Bitcoin or Houses – What is the best investment?
Different investment options carry different risks and return potential over the medium to long term. This study looks at long-term, inflation adjusted returns on different asset classes. Some popular myths are challenged.
-

Origins of the Industrial Revolution
The invention of the steam engine is often considered as the turning point that triggered the industrial revolution. It enabled massive productivity gains as well as the ability to scale industry from small workshops to large enterprises producing consumer goods at scale. Other key technologies make up the industrial landscape today, such as electricity, transport,…
-

Where do Numbers Come From?
Numbers are an abstract concept that don’t seem to exist naturally in our brains or in the real world. The theory of numbers consumes whole books trying to find their origin. Are numbers invented or real?
-
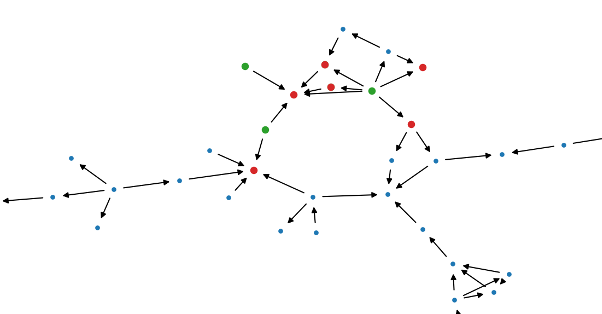
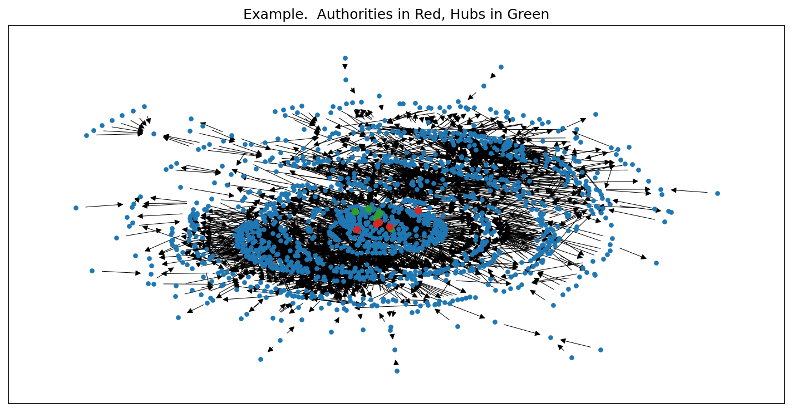
Patent Citation Analysis
Can we learn something about the development of technology and dissemination of ideas by using data science to explore patent citation networks.
-

Transition to Clean Energy Vehicles in Switzerland
Sales of EVs are increasing, but how long will it take before the majority of vehicles on the road are EVs, and how much CO2 will this really displace? This study models the long-term rate of transition to EVs in a typical European market.
-
Too much data, not enough scientists
Data science is at the intersection of programming, mathematics and business or domain knowledge. With the recent explosion of tools and data, it has become much easier to process data. But do programmers really understand the science of data?